Hello!

Welcome to Alex K's portfolio site. Below you can find a bunch of sections with samples of my work. Those marked with (WIP) means that Work In Progress, and it has not been finished yet, but if you have enough courage, you can glimpse inside. 😊

Business Systems Analyst (BSA)

OrderWeb

BSA portfolio project artifacts

In this document you can find group of artifacts that were created at the end of the first Business Systems Analyst interview session with Stakeholders on a future project.

Project documentations for the Mate Project - (WIP)

Mate (M7; M8; MAY7; mt; MT) project documentations.

P2P space for interactions with your flatmates.

Backbone ideas:

  • booking into shared calendar for shared space, instruments, tools;
  • Democratic approval for used of shared things and booking it;
  • Distribution of shared responsibilities & tasks;
  • Messaging;
  • File exchange;
  • Possibly calls

NB The Project in its early stages and flagged as Work In Progress.

Tech stack (most probably) would be:

  • Rust;
  • Diesel (postgres ?);
  • JavaScript;
  • React.js

Python

r0-bot-U_trebA (WIP)

description:
Extension & Automation tool for LinkedIn users, based on the headless Selenium.

This tool is aiming to improve your experience of building up a connections network on the LinkedIn platform in ethical way and try to avoid violation of the User Agreement. This tool will help you to expand your network, by mimicking natural users' behaviour with randomized delays between the interactions with the site and stay within the platform's limits, so you wouldn't face restrictions for your account.

Rust

Handpicked highlights that I've most enjoyed solving

Affine Cipher

description:

Create an implementation of the affine cipher, an ancient encryption system created in the Middle East.

The affine cipher is a type of monoalphabetic substitution cipher. Each character is mapped to its numeric equivalent, encrypted with a mathematical function and then converted to the letter relating to its new numeric value. Although all monoalphabetic ciphers are weak, the affine cypher is much stronger than the atbash cipher, because it has many more keys.

The encryption function is:

E(x) = (ax + b) mod m - where x is the letter's index from 0 - length of alphabet - 1 - m is the length of the alphabet. For the roman alphabet m == 26. - and a and b make the key

The decryption function is:

D(y) = a^-1(y - b) mod m - where y is the numeric value of an encrypted letter, ie. y = E(x) - it is important to note that a^-1 is the modular multiplicative inverse of a mod m - the modular multiplicative inverse of a only exists if a and m are coprime.

To find the MMI of a:

an mod m = 1 - where n is the modular multiplicative inverse of a mod m

More information regarding how to find a Modular Multiplicative Inverse and what it means can be found here.

Because automatic decryption fails if a is not coprime to m your program should return status 1 and "Error: a and m must be coprime." if they are not. Otherwise it should encode or decode with the provided key.

The Caesar (shift) cipher is a simple affine cipher where a is 1 and b as the magnitude results in a static displacement of the letters. This is much less secure than a full implementation of the affine cipher.

Ciphertext is written out in groups of fixed length, the traditional group size being 5 letters, and punctuation is excluded. This is to make it harder to guess things based on word boundaries.

General Examples

  • Encoding test gives ybty with the key a=5 b=7
  • Decoding ybty gives test with the key a=5 b=7
  • Decoding ybty gives lqul with the wrong key a=11 b=7
  • Decoding kqlfd jzvgy tpaet icdhm rtwly kqlon ubstx
  • gives thequickbrownfoxjumpsoverthelazydog with the key a=19 b=13
  • Encoding test with the key a=18 b=13
  • gives Error: a and m must be coprime.
  • because a and m are not relatively prime

Examples of finding a Modular Multiplicative Inverse (MMI)

  • simple example:
    • 9 mod 26 = 9
    • 9 * 3 mod 26 = 27 mod 26 = 1
    • 3 is the MMI of 9 mod 26
  • a more complicated example:
    • 15 mod 26 = 15
    • 15 * 7 mod 26 = 105 mod 26 = 1
    • 7 is the MMI of 15 mod 26

Based on

Wikipedia - https://en.wikipedia.org/wiki/Affine_cipher

Run-Length Encoding

description:

Implement run-length encoding and decoding.

Run-length encoding (RLE) is a simple form of data compression, where runs (consecutive data elements) are replaced by just one data value and count.

For example we can represent the original 53 characters with only 13.

"WWWWWWWWWWWWBWWWWWWWWWWWWBBBWWWWWWWWWWWWWWWWWWWWWWWWB"  ->  "12WB12W3B24WB"

RLE allows the original data to be perfectly reconstructed from the compressed data, which makes it a lossless data compression.

"AABCCCDEEEE"  ->  "2AB3CD4E"  ->  "AABCCCDEEEE"

Based on

Wikipedia - https://en.wikipedia.org/wiki/Run-length_encoding

Atbash Cipher

description:

Create an implementation of the atbash cipher, an ancient encryption system created in the Middle East.

The Atbash cipher is a simple substitution cipher that relies on transposing all the letters in the alphabet such that the resulting alphabet is backwards. The first letter is replaced with the last letter, the second with the second-last, and so on.

An Atbash cipher for the Latin alphabet would be as follows:

Plain:  abcdefghijklmnopqrstuvwxyz
Cipher: zyxwvutsrqponmlkjihgfedcba

It is a very weak cipher because it only has one possible key, and it is a simple mono-alphabetic substitution cipher. However, this may not have been an issue in the cipher's time.

Ciphertext is written out in groups of fixed length, the traditional group size being 5 letters, and punctuation is excluded. This is to make it harder to guess things based on word boundaries.

Examples

  • Encoding test gives gvhg
  • Decoding gvhg gives test
  • Decoding gsvjf rxpyi ldmul cqfnk hlevi gsvoz abwlt gives thequickbrownfoxjumpsoverthelazydog

Based on

Wikipedia - https://en.wikipedia.org/wiki/Atbash

Rotational Cipher aka Caesar cipher

description:

Create an implementation of the rotational cipher, also sometimes called the Caesar cipher.

The Caesar cipher is a simple shift cipher that relies on transposing all the letters in the alphabet using an integer key between 0 and 26. Using a key of 0 or 26 will always yield the same output due to modular arithmetic. The letter is shifted for as many values as the value of the key.

The general notation for rotational ciphers is ROT + <key>. The most commonly used rotational cipher is ROT13.

A ROT13 on the Latin alphabet would be as follows:

Plain:  abcdefghijklmnopqrstuvwxyz
Cipher: nopqrstuvwxyzabcdefghijklm

It is stronger than the Atbash cipher because it has 27 possible keys, and 25 usable keys.

Ciphertext is written out in the same formatting as the input including spaces and punctuation.

Examples

  • ROT5 omg gives trl
  • ROT0 c gives c
  • ROT26 Cool gives Cool
  • ROT13 The quick brown fox jumps over the lazy dog. gives Gur dhvpx oebja sbk whzcf bire gur ynml qbt.
  • ROT13 Gur dhvpx oebja sbk whzcf bire gur ynml qbt. gives The quick brown fox jumps over the lazy dog.

Based on

Wikipedia - https://en.wikipedia.org/wiki/Caesar_cipher

Luhn algorithm

description:

Given a number determine whether or not it is valid per the Luhn formula.

The Luhn algorithm is a simple checksum formula used to validate a variety of identification numbers, such as credit card numbers and Canadian Social Insurance Numbers.

The task is to check if a given string is valid.

Validating a Number

Strings of length 1 or less are not valid. Spaces are allowed in the input, but they should be stripped before checking. All other non-digit characters are disallowed.

Example 1: valid credit card number

4539 3195 0343 6467

The first step of the Luhn algorithm is to double every second digit, starting from the right. We will be doubling

4_3_ 3_9_ 0_4_ 6_6_

If doubling the number results in a number greater than 9 then subtract 9 from the product. The results of our doubling:

8569 6195 0383 3437

Then sum all the digits:

8+5+6+9+6+1+9+5+0+3+8+3+3+4+3+7 = 80

If the sum is evenly divisible by 10, then the number is valid. This number is valid!

Example 2: invalid credit card number

8273 1232 7352 0569

Double the second digits, starting from the right

7253 2262 5312 0539

Sum the digits

7+2+5+3+2+2+6+2+5+3+1+2+0+5+3+9 = 57

57 is not evenly divisible by 10, so this number is not valid.

Based on

The Luhn Algorithm on Wikipedia - https://en.wikipedia.org/wiki/Luhn_algorithm

Poker

description:

Pick the best hand(s) from a list of poker hands.

See wikipedia for an overview of poker hands.

  • Ranking a list of poker hands can be considered a sorting problem.
  • Rust provides the sort method for Vec<T> where T: Ord.
  • Ord types form a total order: exactly one of a < b, a == b, or a > b must be true.
  • Poker hands do not conform to a total order: it is possible for two hands to be non-equal but have equal sort order. Example: "3S 4S 5D 6H JH", "3H 4H 5C 6C JD".
  • Rust provides the PartialOrd trait to handle the case of sortable things which do not have a total order. However, it doesn't provide a standard sort method for Vec<T> where T: PartialOrd. The standard idiom to sort a vector in this case is your_vec.sort_by(|a, b| a.partial_cmp(b).unwrap_or(Ordering::{Less|Equal|Greater}));, depending on your needs.
  • You might consider implementing a type representing a poker hand which implements PartialOrd.

Scale Generator

description:

Given a tonic, or starting note, and a set of intervals, generate
the musical scale starting with the tonic and following the
specified interval pattern.

Scales in Western music are based on the chromatic (12-note) scale. This scale can be expressed as the following group of pitches:

A, A#, B, C, C#, D, D#, E, F, F#, G, G#

A given sharp note (indicated by a #) can also be expressed as the flat of the note above it (indicated by a b) so the chromatic scale can also be written like this:

A, Bb, B, C, Db, D, Eb, E, F, Gb, G, Ab

The major and minor scale and modes are subsets of this twelve-pitch collection. They have seven pitches, and are called diatonic scales. The collection of notes in these scales is written with either sharps or flats, depending on the tonic. Here is a list of which are which:

No Sharps or Flats:

C major
a minor

Use Sharps:

G, D, A, E, B, F# major
e, b, f#, c#, g#, d# minor

Use Flats:

F, Bb, Eb, Ab, Db, Gb major
d, g, c, f, bb, eb minor

The diatonic scales, and all other scales that derive from the chromatic scale, are built upon intervals. An interval is the space between two pitches.

The simplest interval is between two adjacent notes, and is called a "half step", or "minor second" (sometimes written as a lower-case "m"). The interval between two notes that have an interceding note is called a "whole step" or "major second" (written as an upper-case "M"). The diatonic scales are built using only these two intervals between adjacent notes.

Non-diatonic scales can contain other intervals. An "augmented second" interval, written "A", has two interceding notes (e.g., from A to C or Db to E) or a "whole step" plus a "half step". There are also smaller and larger intervals, but they will not figure into this exercise.

Simple Cipher

description:

Implement a simple shift cipher like Caesar and a more secure substitution cipher.

Step 1

"If he had anything confidential to say, he wrote it in cipher, that is, by so changing the order of the letters of the alphabet, that not a word could be made out. If anyone wishes to decipher these, and get at their meaning, he must substitute the fourth letter of the alphabet, namely D, for A, and so with the others." —Suetonius, Life of Julius Caesar

Ciphers are very straight-forward algorithms that allow us to render text less readable while still allowing easy deciphering. They are vulnerable to many forms of cryptanalysis, but we are lucky that generally our little sisters are not crypt-analysts.

The Caesar Cipher was used for some messages from Julius Caesar that were sent afield. Now Caesar knew that the cipher wasn't very good, but he had one ally in that respect: almost nobody could read well. So even being a couple letters off was sufficient so that people couldn't recognize the few words that they did know.

Your task is to create a simple shift cipher like the Caesar Cipher. This image is a great example of the Caesar Cipher:

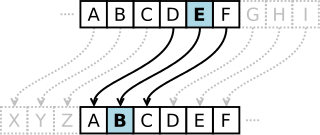
Caesar Cipher

For example:

Giving iamapandabear as input to the encode function returns the cipher ldpdsdqgdehdu. Obscure enough to keep our message secret in transit.

When ldpdsdqgdehdu is put into the decode function it would return the original iamapandabear letting your friend read your original message.

Step 2

Shift ciphers are no fun though when your kid sister figures it out. Try amending the code to allow us to specify a key and use that for the shift distance. This is called a substitution cipher.

Here's an example:

Given the key aaaaaaaaaaaaaaaaaa, encoding the string iamapandabear would return the original iamapandabear.

Given the key ddddddddddddddddd, encoding our string iamapandabear would return the obscured ldpdsdqgdehdu

In the example above, we've set a = 0 for the key value. So when the plaintext is added to the key, we end up with the same message coming out. So aaaa is not an ideal key. But if we set the key to dddd, we would get the same thing as the Caesar Cipher.

Step 3

The weakest link in any cipher is the human being. Let's make your substitution cipher a little more fault-tolerant by providing a source of randomness and ensuring that the key contains only lowercase letters.

If someone doesn't submit a key at all, generate a truly random key of at least 100 lowercase characters in length.

Based on

Substitution Cipher at Wikipedia - http://en.wikipedia.org/wiki/Substitution_cipher

Nth Prime

description:

Given a number n, determine what the nth prime is.

By listing the first six prime numbers: 2, 3, 5, 7, 11, 13, we can see that the 6th prime is 13.

If your language provides methods in the standard library to deal with prime numbers, pretend they don't exist and implement them yourself.

Remember that while people commonly count with 1-based indexing (i.e. "the 6th prime is 13"), many programming languages, including Rust, use 0-based indexing (i.e. primes[5] == 13).

Use 0-based indexing for your implementation.

Based on

A variation on Problem 7 at Project Euler - https://projecteuler.net/problem=7

All my Solved Exercism training exercises